Introduction
Within the text of Bridging Physics and Communications: Experimental Detection and Analysis of Web Site Users’ Paths in an Environment of Free Choice, the thesis I wrote in 2000 for my master of arts degree in journalism, I embedded seven essays that each stand alone, yet work together to present the thoughts underlying the thesis itself. These essays originally served as the content appearing in the test Web site.
This is the third essay.
Essay
Chaos is not the absence of order, but the foundation for emerging complex patterns and behaviors.
Undergraduates who study physics become familiar with the pendulum. They spend a laboratory session measuring the periods of pendula of various lengths to see how period changes with length. They also take a pendulum of a given length and change the mass of the bob, to see what effect various masses have on the period. These measurements provide quantifiable confirmation of the predictive power of the formula they have derived for the period of a pendulum:
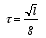
They confirm that, within the limits of their ability to start and stop stopwatches as the bob passes a fixed point on its path and to count swings and to measure the length of the pendulum and to use a pan balance to gauge the weight of the bob, the period really does vary as the square root of the length of the pendulum and is independent of the mass of the bob.
The formula can even be solved for g, for the acceleration due to gravity, and that can be measured. The measurement agrees to several significant figures with the value found by looking for that number in a copy of the CRC Handbook of Chemistry and Physics (David R. Lide, ed., CRC Handbook of Chemistry and Physics, (Boca Raton, Florida: CRC Press, Inc., 1999)). All seems simple and predictable…until the professor asks, “What have we ignored? How have we simplified and idealized the pendulum?”
Then the seeming order of that simple formula dissolves into a seemingly chaotic mess of systems of simultaneous nonlinear differential equations. The simplifications needed to avoid this intractable mathematics are astounding. Students have assumed the pendulum swings like a playground swing, back and forth, but not side to side in a kind of elliptical path. The mass of the pendulum string or wire and its distribution along its length have been neglected. The air resistance retarding the motion of the bob (and the string or wire) has been dropped. The elasticity of the string or wire and any spring-like forces it applies at the pivot point have been deemed too small to count. The stretching of the wire or string as the velocity of the bob varies has been considered negligible. The bob has been idealized as a mass concentrated at a point and not as a real object with distributed mass at varying distances from the pivot point.
When all of these real-life considerations find their way into an attempt to write down the formulae describing the motion, or the behavior, of the pendulum, the formulae become impossible to resolve using traditional mathematical methods. Experimental physicists are left to do what theoretical physicists have historically decried, finding numerical, brute-force, calculated approximations, to describe roughly what the theory, in a theoretical environment, can describe precisely and simply.
Reality has intruded.
There are other places where traditional theoretical physics butts up against reality and looks the worse for the encounter. This physics cannot describe why the smooth flow of water falling from a faucet will turn suddenly rough and dribbly, or why the equally smooth and silent rise of smoke from a cigarette in a totally still room will turn suddenly turbid. Or what happens with the flow of air over an airplane’s wing. Or given a set of meteorological measurements for Tuesday, why the report of the weather on Sunday is at best an estimate and not a prediction with any high degree of certainty.
These challenges and conundrums lie in the realm where classical physics has met it match in the seeming chaos of the real world. But here chaos does not mean what we normally mean by the word. The traditional view of chaos characterizes it as the absence of order, where order is seen as the natural state of affairs and disorder is a deviation from that state. But in recent years, as scientists speak of chaos and seek to study chaotic systems, they refer to a deeper order and structure that lies outside of the boundaries of classical physics as traditionally formulated.
What this means is not that reality is perturbed, but that classical physics is inadequate to describe reality as it exists. In contrast, chaos theorists see the world through special lenses:
Chaos poses problems that defy accepted ways of working in science. It makes strong claims about the universal behavior of complexity. The first chaos theorists, the scientists who set in the discipline in motion, shared certain sensibilities. They had an eye for pattern, especially pattern that appeared on different scales at the same time. They had a taste for randomness and complexity, for jagged edges and sudden leaps. Believers in chaos–and they sometimes called themselves believers, or converts, or evangelists–speculate about determinism and free will, about evolution, about the nature of conscious intelligence. They feel that they are turning back a trend in science toward reductionism, the analysis of systems in terms of their constituent parts: quarks, chromosomes, or neurons. They believe that they are looking for the whole (James Gleick, Chaos: Making a New Science, (New York: Viking Penguin Inc., 1987), 5).
Chaotic systems are characterized by several tendencies. First, small changes in initial conditions can give rise to vastly different outcomes. For example, the slow drip of a faucet changes its timing drastically (and nonlinearly) depending upon minute changes in the volume of water released slowly from the faucet. Second, ordered systems can arise spontaneously from the interactions of many small components following simple rules. For example, geese flying together mind their places relative to the nearest geese; and from this simple rule, the pattern of the V evolves.
From these basic insights into chaos, scientists have begun to speak about terms such as emergence and complexity. By emergence, chaos scientists mean the property of systems that over time, order and structure will evolve naturally as an outgrowth of the interactions within the system. The most famous example of emergent order is the currently held theory of the evolution of life, where self-replicating clays have, over great spans of time, served as the foundation from which all life on earth has developed (If recent speculation that life on Earth was seeded by meteors ejected from Mars following asteroid strikes turns out to be true, it would still not negate the argument for the emergent nature of life, but merely move it to another venue. Michael Paine, “Your Ancestors May Be Martian;” available from http://www.space.com/scienceastronomy/astronomy/rocks_fromspace_991108.html; Internet; accessed 2 September 2000). Emergence, as a property of the Earth as a system, suggests that the development of life, and the evolution of increasingly specialized and complex forms of life, is an inherent characteristic of the Earth as a system, a chaotic system.
Complexity refers to the characteristic of chaotic systems that the relations among the components of the system are not simply reducible to linear relations, but that the connections among those components are accurately expressible only in nonlinear fashion. This means, for example, that one cannot say simply that rainfall varies directly with the relative humidity. But one can say that precipitation levels, relative humidity, the direction and speed of prevailing winds, the location and motion of atmospheric highs and lows, and a host of other components are all interconnected, so that predictions are a matter of modeling a system and not a matter of extrapolating the measurement of a dependent variable from a single independent variable.
One can see these properties—emergence and complexity—exhibited by human systems as well as by “natural” systems. The evolution of the Internet displays these properties. In fact, attempts to impose a specific order and structure upon the system invariably meet with work-arounds, improvisations, and hacks. But, when designers allow a sufficiently large number of interactions to occur in the context of simple rules governing those interactions, spectacularly complex and diversified structures emerge. The Internet itself, based upon a few protocols for the transfer of data, upon the principles of packet-switching and dispersed computing power, has shown remarkable evolutionary achievements in a very short span of time.
And because each subset of the system of the Internet is based upon the same protocols and principles, individual sites can exhibit the same characteristics of complex order emerging from a chaotic system. Typical site design imposes a navigational order on users, and to no one’s surprise, users follow the structure set for them. But if users are presented with free choice within a site, one can expect to see certain complex patterns of behavior emerge as one tracks the choices of users. Their behaviors may seem random, but in reality they are chaotic. And chaos is not the absence of order, but the foundation for emerging complex patterns and behaviors.
Chaos is not the absence of order, but the foundation for emerging complex patterns and behaviors.